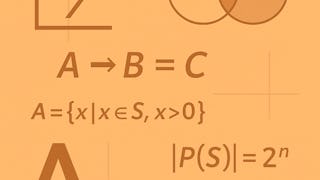Discrete mathematics forms the mathematical foundation of computer and information science. It is also a fascinating subject in itself.
Learners will become familiar with a broad range of mathematical objects like sets, functions, relations, graphs, that are omnipresent in computer science. Perhaps more importantly, they will reach a certain level of mathematical maturity - being able to understand formal statements and their proofs; coming up with rigorous proofs themselves; and coming up with interesting results. This course attempts to be rigorous without being overly formal. This means, for every concept we introduce we will show at least one interesting and non-trivial result and give a full proof. However, we will do so without too much formal notation, employing examples and figures whenever possible. The main topics of this course are (1) sets, functions, relations, (2) enumerative combinatorics, (3) graph theory, (4) network flow and matchings. It does not cover modular arithmetic, algebra, and logic, since these topics have a slightly different flavor and because there are already several courses on Coursera specifically on these topics.