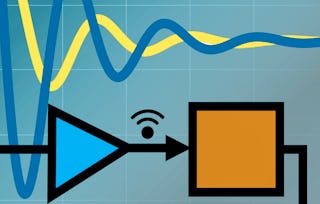
In this course, you'll explore modeling of dynamic systems and feedback control. The course begins with an introduction of control theory and the application of Laplace transforms in solving differential equations, providing a strong foundation in linearity, time-invariance, and dynamic system modeling. The following week will delve into the laws governing the modeling of dynamic systems, with a focus on deriving differential equations from fundamental principles like Newton's laws and Kirchhoff's laws, as well as mastering the representation of systems as transfer functions in the Laplace domain. The third week delves deeper into Laplace transforms, emphasizing initial/final value theorems, block diagram manipulation, and dynamic response analysis. Moving into the fourth week, you'll learn to analyze system performance using transient step response specifications, enabling you to assess and optimize system behavior effectively. Finally, in the fifth week, you'll explore Bounded-Input Bounded-Output (BIBO) stability and Routh's stability criterion, gaining the skills to assess, analyze, and design stable systems. By the course's end, you'll be well-equipped to navigate the intricacies of control systems and dynamic modeling.

Control Systems Analysis: Modeling of Dynamic Systems

Control Systems Analysis: Modeling of Dynamic Systems

Instructor: Dr. Lucy Pao
Access provided by ITC-Infotech
10,921 already enrolled
117 reviews
Recommended experience
What you'll learn
Derive differential equations and transfer functions for simple mechanical, electrical, and electromechanical systems.
Analyze the dynamic response of 1st and 2nd order systems.
Explain the relationship between pole locations of 2nd-order systems and common step response performance specifications.
Characterize Bounded-Input Bounded-Output (BIBO) stability and determine the number of unstable roots using Routh’s stability criterion.
Skills you'll gain
Details to know

Add to your LinkedIn profile
11 assignments
See how employees at top companies are mastering in-demand skills

There are 5 modules in this course
Welcome to Modeling Feedback Systems. This first week combines the essential concepts of control systems and differential equations. You will explore the foundations of control theory, understand the significance of feedback control, and master the application of Laplace transforms in solving ordinary differential equations. By the end of this week, you will possess a solid understanding of linearity, time-invariance, modeling approaches, and the practical uses of control systems.
What's included
9 videos1 reading3 assignments
During the second week of this course, you will delve into the foundational laws used in modeling feedback systems. You will explore how these laws are applied to model simple mechanical, electrical, and electromechanical systems by deriving differential equations from fundamental principles such as Newton's laws of motion, Kirchhoff's laws, and the Motor/Generator laws. Additionally, you will gain proficiency in representing these systems as transfer functions using Laplace and inverse Laplace transforms, which will enable you to analyze and understand their behavior in the frequency domain. By the end of this week, you will have acquired the essential knowledge and skills to effectively model and analyze a wide range of dynamic systems.
What's included
10 videos1 assignment
In the third week of this course, you will dive deeper into the application of Laplace transforms. You will start by learning how to use the initial/final value theorems to calculate the values of time-domain signals using their Laplace-domain representation. Additionally, you will develop the skills to manipulate block diagram representations of interconnected systems, enabling you to analyze complex systems and understand their overall behavior. You will also explore the dynamic response of 1st- and 2nd-order systems, gaining insights into their transient and steady-state characteristics. Lastly, you will discover techniques to approximate higher-order systems reasonably well by utilizing the impulse and step responses of lower-order systems. By the end of this week, you will have acquired advanced tools and techniques to analyze and model a wide range of dynamic systems with precision and accuracy.
What's included
9 videos2 assignments
In the fourth week of this course, you will focus on system performance analysis using transient step response specifications. You will learn how to calculate and evaluate key performance metrics such as rise time, settling time, and overshoot using the step response of a system. By understanding the relationship between pole locations and step response performance specifications, you will gain insights into how system dynamics affect the overall performance. Furthermore, you will utilize transient step response data to estimate the 2nd-order transfer function approximation, enabling you to model and analyze complex systems accurately. Lastly, you will compare the impact of zeros and additional poles on the step responses of systems, deepening your understanding of how system components influence the overall behavior. By the end of this week, you will be equipped with the skills to assess and optimize system performance based on transient step response characteristics.
What's included
12 videos2 assignments
Congratulations on making it to the 5th and final week of this course. This week you will delve into the concept of Bounded-Input Bounded-Output (BIBO) stability and its application in analyzing Linear Time-Invariant (LTI) systems. You will learn the necessary and sufficient conditions for BIBO stability and apply them to assess the stability of dynamic systems. Additionally, you will explore Routh's stability criterion, which allows you to determine system stability. Furthermore, you will discover how to design stable proportional-feedback systems using Routh's stability criterion, enabling you to create control systems that exhibit desirable behavior. By the end of this week, you will have acquired the knowledge and skills to analyze, assess, and design stable systems using BIBO stability and Routh's stability criterion.
What's included
10 videos3 assignments
Build toward a degree
This course is part of the following degree program(s) offered by University of Colorado Boulder. If you are admitted and enroll, your completed coursework may count toward your degree learning and your progress can transfer with you.¹
Instructor

Offered by
Why people choose Coursera for their career

Felipe M.

Jennifer J.

Larry W.

Chaitanya A.
Learner reviews
- 5 stars
75.21%
- 4 stars
19.65%
- 3 stars
3.41%
- 2 stars
0%
- 1 star
1.70%
Showing 3 of 117
Reviewed on Oct 26, 2025
in the course, some questions were hard to understand. For future courses if possible, add conceptual hints for solving the problems.
Reviewed on Nov 16, 2024
Thanks to dr Lucy pao never seen a teacher like him
Reviewed on Mar 19, 2024
Fairly good class. Students with experience in diff eqs should find it challenging. I would recommend creating extra material in using software like Mathematica or Matlab to help solve problems.
Explore more from Physical Science and Engineering

Università di Napoli Federico II
Università di Napoli Federico II