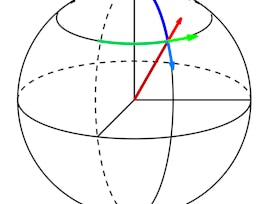
This course trains you in the skills needed to program specific orientation and achieve precise aiming goals for spacecraft moving through three dimensional space. First, we cover stability definitions of nonlinear dynamical systems, covering the difference between local and global stability. We then analyze and apply Lyapunov's Direct Method to prove these stability properties, and develop a nonlinear 3-axis attitude pointing control law using Lyapunov theory. Finally, we look at alternate feedback control laws and closed loop dynamics.



Control of Nonlinear Spacecraft Attitude Motion
This course is part of Spacecraft Dynamics and Control Specialization

Instructor: Hanspeter Schaub
Sponsored by Taipei Medical University [C4CB]
9,460 already enrolled
(68 reviews)
What you'll learn
Differentiate between a range of nonlinear stability concepts
Apply Lyapunov’s direct method to argue stability and convergence on a range of dynamical systems
Develop rate and attitude error measures for a 3-axis attitude control using Lyapunov theory
Analyze rigid body control convergence with unmodeled torque
Skills you'll gain
Details to know

Add to your LinkedIn profile
22 assignments
See how employees at top companies are mastering in-demand skills

Build your subject-matter expertise
- Learn new concepts from industry experts
- Gain a foundational understanding of a subject or tool
- Develop job-relevant skills with hands-on projects
- Earn a shareable career certificate


Earn a career certificate
Add this credential to your LinkedIn profile, resume, or CV
Share it on social media and in your performance review

There are 4 modules in this course
Discusses stability definitions of nonlinear dynamical systems, and compares to the classical linear stability definitions. The difference between local and global stability is covered.
What's included
12 videos7 assignments
Lyapunov's direct method is employed to prove these stability properties for a nonlinear system and prove stability and convergence. The possible function definiteness is introduced which forms the building block of Lyapunov's direct method. Convenient prototype Lyapunov candidate functions are presented for rate- and state-error measures.
What's included
14 videos7 assignments
A nonlinear 3-axis attitude pointing control law is developed and its stability is analyized using Lyapunov theory. Convergence is discussed considering both modeled and unmodeled torques. The control gain selection is presented using the convenient linearized closed loop dynamics.
What's included
8 videos5 assignments
Alternate feedback control laws are formulated where actuator saturation is considered. Further, a control law is presented that perfectly linearizes the closed loop dynamics in terms of quaternions and MRPs. Finally, the 3-axis Lyapunov attitude control is developed for a spacecraft with a cluster of N reaction wheel control devices.
What's included
6 videos3 assignments1 peer review
Instructor

Offered by
Why people choose Coursera for their career




Learner reviews
68 reviews
- 5 stars
82.35%
- 4 stars
8.82%
- 3 stars
4.41%
- 2 stars
4.41%
- 1 star
0%
Showing 3 of 68
Reviewed on Sep 18, 2020
Excellent course but it could have been smoother if the instructor kept himself in loop with people doing the course
Reviewed on Nov 26, 2020
The whole course is really good. The instructor is awesome at teaching concepts. I got to learn a lot of new things.
Reviewed on May 29, 2019
Excellent course! Enjoyed it a lot. Learnt a lot as well. Thank you.
Recommended if you're interested in Physical Science and Engineering
The Hong Kong University of Science and Technology

University of Colorado Boulder

University of Arizona

University of Michigan

Open new doors with Coursera Plus
Unlimited access to 10,000+ world-class courses, hands-on projects, and job-ready certificate programs - all included in your subscription
Advance your career with an online degree
Earn a degree from world-class universities - 100% online
Join over 3,400 global companies that choose Coursera for Business
Upskill your employees to excel in the digital economy