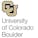This course will focus on theory and implementation of hypothesis testing, especially as it relates to applications in data science. Students will learn to use hypothesis tests to make informed decisions from data. Special attention will be given to the general logic of hypothesis testing, error and error rates, power, simulation, and the correct computation and interpretation of p-values. Attention will also be given to the misuse of testing concepts, especially p-values, and the ethical implications of such misuse.



Statistical Inference and Hypothesis Testing in Data Science Applications
This course is part of Data Science Foundations: Statistical Inference Specialization

Instructor: Jem Corcoran
Sponsored by IEM UEM Group
6,632 already enrolled
(48 reviews)
Recommended experience
What you'll learn
Define a composite hypothesis and the level of significance for a test with a composite null hypothesis.
Define a test statistic, level of significance, and the rejection region for a hypothesis test. Give the form of a rejection region.
Perform tests concerning a true population variance.
Compute the sampling distributions for the sample mean and sample minimum of the exponential distribution.
Skills you'll gain
Details to know

Add to your LinkedIn profile
1 quiz, 5 assignments
See how employees at top companies are mastering in-demand skills

Build your subject-matter expertise
- Learn new concepts from industry experts
- Gain a foundational understanding of a subject or tool
- Develop job-relevant skills with hands-on projects
- Earn a shareable career certificate


Earn a career certificate
Add this credential to your LinkedIn profile, resume, or CV
Share it on social media and in your performance review

There are 6 modules in this course
Welcome to the course! This module contains logistical information to get you started!
What's included
3 readings1 discussion prompt1 ungraded lab
In this module, we will define a hypothesis test and develop the intuition behind designing a test. We will learn the language of hypothesis testing, which includes definitions of a null hypothesis, an alternative hypothesis, and the level of significance of a test. We will walk through a very simple test.
What's included
6 videos11 readings1 quiz1 programming assignment2 ungraded labs
In this module, we will expand the lessons of Module 1 to composite hypotheses for both one and two-tailed tests. We will define the “power function” for a test and discuss its interpretation and how it can lead to the idea of a “uniformly most powerful” test. We will discuss and interpret “p-values” as an alternate approach to hypothesis testing.
What's included
7 videos7 readings1 assignment1 programming assignment1 ungraded lab
In this module, we will learn about the chi-squared and t distributions and their relationships to sampling distributions. We will learn to identify when hypothesis tests based on these distributions are appropriate. We will review the concept of sample variance and derive the “t-test”. Additionally, we will derive our first two-sample test and apply it to make some decisions about real data.
What's included
7 videos7 readings1 assignment1 programming assignment1 ungraded lab
In this module, we will consider some problems where the assumption of an underlying normal distribution is not appropriate and will expand our ability to construct hypothesis tests for this case. We will define the concept of a “uniformly most powerful” (UMP) test, whether or not such a test exists for specific problems, and we will revisit some of our earlier tests from Modules 1 and 2 through the UMP lens. We will also introduce the F-distribution and its role in testing whether or not two population variances are equal.
What's included
6 videos6 readings2 assignments
In this module, we develop a formal approach to hypothesis testing, based on a “likelihood ratio” that can be more generally applied than any of the tests we have discussed so far. We will pay special attention to the large sample properties of the likelihood ratio, especially Wilks’ Theorem, that will allow us to come up with approximate (but easy) tests when we have a large sample size. We will close the course with two chi-squared tests that can be used to test whether the distributional assumptions we have been making throughout this course are valid.
What's included
5 videos5 readings1 assignment1 programming assignment1 ungraded lab
Instructor

Offered by
Why people choose Coursera for their career




Learner reviews
48 reviews
- 5 stars
79.59%
- 4 stars
14.28%
- 3 stars
4.08%
- 2 stars
0%
- 1 star
2.04%
Showing 3 of 48
Reviewed on Jul 27, 2022
Loved the material. Content looks quite convincing and well explained!
Reviewed on Oct 26, 2022
In-depth course on Hypothesis testing. Course instructor is quite engaging.
Reviewed on Feb 8, 2024
Great course, challenging quizzes. Labs and programming assignments are really helpful, especially the one on Wilks theorem, I really liked that one.
Recommended if you're interested in Data Science

University of Colorado Boulder

University of Colorado Boulder


University of Colorado Boulder


University of Colorado Boulder

Open new doors with Coursera Plus
Unlimited access to 10,000+ world-class courses, hands-on projects, and job-ready certificate programs - all included in your subscription
Advance your career with an online degree
Earn a degree from world-class universities - 100% online
Join over 3,400 global companies that choose Coursera for Business
Upskill your employees to excel in the digital economy