Ce cours est une introduction à l'analyse complexe, qui est la théorie des fonctions complexes d'une variable complexe. Nous commencerons par introduire le plan complexe, ainsi que l'algèbre et la géométrie des nombres complexes, puis nous nous frayerons un chemin à travers la différenciation, l'intégration, la dynamique complexe, la représentation des séries de puissance et les séries de Laurent dans des territoires à la limite de ce qui est connu aujourd'hui. Chaque module se compose de cinq conférences vidéo avec des quiz intégrés, suivis d'un devoir noté électroniquement. En outre, les modules 1, 3 et 5 contiennent également une évaluation par les pairs.

Introduction à l’analyse complexe
Saisissez l'occasion de faire des économies ! Bénéficiez de 40 % de réduction sur 3 mois de Coursera Plus et d'un accès complet à des milliers de cours.

Introduction à l’analyse complexe

Instructeur : Dr. Petra Bonfert-Taylor
Enseignant de premier plan
75 263 déjà inscrits
Inclus avec
1,091 avis
Compétences que vous acquerrez
- Catégorie : Algebra
- Catégorie : Trigonometry
- Catégorie : Integral Calculus
- Catégorie : Advanced Mathematics
- Catégorie : Geometry
- Catégorie : Calculus
- Catégorie : Graphing
- Catégorie : Mathematical Theory & Analysis
Détails à connaître

Ajouter à votre profil LinkedIn
Découvrez comment les employés des entreprises prestigieuses maîtrisent des compétences recherchées

Il y a 8 modules dans ce cours
Nous commencerons ce module par un bref aperçu de l'histoire des nombres complexes : Quand et pourquoi ont-ils été inventés ? En particulier, nous examinerons le fait plutôt surprenant que le besoin initial de nombres complexes n'est pas né de l'étude d'équations quadratiques (comme la résolution de l'équation z^2+1 = 0), mais plutôt de l'étude d'équations cubiques ! Ensuite, nous aborderons l'algèbre et la géométrie dans le plan complexe afin d'apprendre à calculer et à visualiser les nombres complexes. À cette fin, nous apprendrons également la représentation polaire des nombres complexes, qui se prête bien à la recherche des racines des nombres complexes. Nous terminerons ce module par un peu de topologie dans le plan complexe.
Inclus
5 vidéos5 lectures1 devoir1 évaluation par les pairs
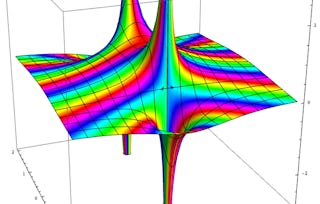
L'analyse complexe est l'étude des fonctions qui vivent dans le plan complexe, c'est-à-dire des fonctions qui ont des arguments et des résultats complexes. L'objectif principal de ce module est de nous familiariser avec ces fonctions. En fin de compte, nous voudrons étudier leurs propriétés de lissage (c'est-à-dire que nous voudrons différencier des fonctions complexes de variables complexes), et nous devons donc comprendre les suites de nombres complexes ainsi que les limites dans le plan complexe. Nous utiliserons les polynômes quadratiques comme exemple dans l'étude des fonctions complexes et nous ferons une excursion dans le magnifique domaine de la dynamique complexe en examinant les itérés de certains polynômes quadratiques. Cela nous permet d'apprendre les bases de la construction des ensembles de Julia des polynômes quadratiques. Vous apprendrez tout ce que vous devez savoir pour créer vos propres images fractales, si vous le souhaitez. Nous terminerons ce module en définissant et en examinant l'ensemble de Mandelbrot et l'une des plus grandes conjectures en suspens dans le domaine de la dynamique complexe.
Inclus
5 vidéos5 lectures1 devoir
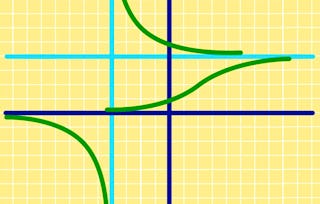
Lorsque nous étudions les fonctions, nous nous intéressons souvent à leur comportement local, plus précisément à la façon dont les fonctions changent lorsque leur argument change. Cela nous amène à étudier la différenciation complexe, un concept plus puissant que celui que nous avons appris en calcul. Nous commencerons ce module en révisant quelques notions de calcul, puis nous nous familiariserons avec la différenciation complexe et les équations de Cauchy-Riemann afin de rencontrer les principaux acteurs : les fonctions analytiques. Il s'agit de fonctions qui possèdent des dérivées complexes en de nombreux endroits, ce qui leur confère certaines des plus belles propriétés que les mathématiques puissent offrir. Nous terminerons ce module par l'étude de certaines fonctions complexes différentiables, telles que la fonction exponentielle complexe et les fonctions trigonométriques complexes. Ces fonctions s'accordent avec leurs homologues à valeurs réelles bien connues sur l'axe des réels !
Inclus
5 vidéos5 lectures1 devoir1 évaluation par les pairs
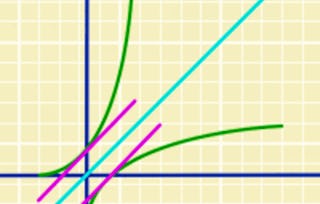
Nous commencerons ce module en étudiant les fonctions inverses des fonctions analytiques telles que le logarithme complexe (inverse de l'exponentielle) et les racines complexes (inverses des puissances). Pour posséder un inverse (local), une fonction analytique doit avoir une dérivée non nulle, et nous découvrirons le fait puissant qu'en un tel endroit, une fonction analytique préserve les angles entre les courbes et est donc une cartographie conforme ! Nous consacrerons deux cours à des mappings conformes très particuliers, à savoir les transformations de Möbius ; il s'agit de certains des mappings les plus fondamentaux de l'analyse géométrique. Nous terminerons ce module avec le célèbre et étonnant théorème de Riemann sur les cartographies. Ce théorème nous permet d'étudier des sous-régions arbitraires simplement connectées du plan complexe en transportant la géométrie et l'analyse complexe du disque unitaire vers ces domaines via des mappings conformes, dont l'existence est garantie par le théorème des mappings de Riemann.
Inclus
5 vidéos5 lectures1 devoir
Maintenant que nous sommes familiarisés avec la différenciation complexe et les fonctions analytiques, nous sommes prêts à aborder l'intégration. Mais nous sommes dans le plan complexe, alors quels sont les objets sur lesquels nous allons intégrer ? Les courbes ! Nous commencerons ce module par étudier les courbes ("chemins") et nous nous familiariserons ensuite avec l'intégrale de chemin complexe. Ensuite, nous découvrirons le magnifique théorème et la formule de l'intégrale de Cauchy, qui englobe tout. Nous étudierons ensuite certaines des conséquences puissantes de ces théorèmes, telles que le théorème de Liouville, le principe du maximum et, croyez-le ou non, nous serons en mesure de prouver le théorème fondamental de l'algèbre à l'aide de l'analyse complexe. La semaine s'annonce riche en résultats étonnants !
Inclus
5 vidéos5 lectures1 devoir1 évaluation par les pairs
Dans ce module, nous apprendrons à connaître les représentations en séries de puissance des fonctions analytiques. Nous commencerons par étudier les séries infinies de nombres complexes et de fonctions complexes ainsi que leurs propriétés de convergence. Les séries de puissances sont particulièrement faciles à comprendre, se comportent bien et sont faciles à utiliser. Nous apprendrons que toute fonction analytique peut être représentée localement sous la forme d'une série de puissances, ce qui permet d'approximer localement les fonctions analytiques à l'aide de polynômes. Nous explorerons la fonction zêta de Riemann et nous nous pencherons sur des sujets à la limite de ce qui est connu aujourd'hui, comme l'hypothèse de Riemann et sa relation avec les nombres premiers.
Inclus
5 vidéos5 lectures1 devoir
Les séries de Laurent sont un outil puissant pour comprendre les fonctions analytiques près de leurs singularités. Alors que les séries de puissance avec des exposants non négatifs peuvent être utilisées pour représenter les fonctions analytiques dans les disques, les séries de Laurent (qui peuvent avoir des exposants négatifs) servent un objectif similaire dans les anneaux. Nous commencerons ce module en introduisant les séries de Laurent et leur relation avec les fonctions analytiques, puis nous poursuivrons avec l'étude et la classification des singularités isolées des fonctions analytiques. Nous rencontrerons quelques théorèmes puissants et célèbres tels que le théorème de Casorati-Weierstraß et le théorème de Picard, qui servent tous deux à mieux comprendre le comportement d'une fonction analytique près d'une singularité essentielle. Enfin, nous serons prêts à aborder le théorème des résidus, qui a de nombreuses applications importantes. Nous apprendrons à trouver les résidus et à évaluer certaines intégrales (même certaines intégrales réelles sur la droite réelle !) grâce à cet important théorème.
Inclus
6 vidéos6 lectures1 devoir
Félicitations pour avoir terminé les sept semaines de ce cours ! Ce module contient l'examen final du cours. L'examen est cumulatif et couvre les sujets abordés au cours des semaines 1 à 7. L'examen comporte 20 questions et est conçu pour durer deux heures. Vous n'avez droit qu'à une seule tentative, mais vous n'êtes pas obligé de terminer l'examen en deux heures. Le forum de discussion restera ouvert pendant l'examen. Il est contraire au code d'honneur de discuter des réponses aux questions de l'examen sur le forum. Le forum ne doit être utilisé que pour discuter de questions relatives à d'autres matières ou pour signaler au personnel des problèmes techniques liés à l'examen.
Inclus
1 devoir
Instructeur

Offert par
En savoir plus sur Mathématiques et logique
 Statut : Essai gratuit
Statut : Essai gratuitJohns Hopkins University
The University of Sydney
 Statut : Prévisualisation
Statut : PrévisualisationThe University of Sydney
 Statut : Essai gratuit
Statut : Essai gratuitThe Hong Kong University of Science and Technology
Pour quelles raisons les étudiants sur Coursera nous choisissent-ils pour leur carrière ?

Felipe M.

Jennifer J.

Larry W.

Chaitanya A.
Avis des étudiants
- 5 stars
85,80 %
- 4 stars
12,36 %
- 3 stars
1,19 %
- 2 stars
0,09 %
- 1 star
0,54 %
Affichage de 3 sur 1091
Révisé le 2 août 2023
Thank you for providing the fundamentals of the complex analysis course, I hope it will give me enough preparations for the actual course I'm going to take in my college.
Révisé le 5 avr. 2018
The lectures were very easy to follow and the exercises fitted these lectures well. This course was not always very rigorous, but a great introduction to complex analysis nevertheless. Thank you!
Révisé le 23 sept. 2017
Wow, great introductory course on complex analysis, was hoping for a bit more analysis and a bit more actual proofs, but it's Coursera, can't expect a full-on course here.

Ouvrez de nouvelles portes avec Coursera Plus
Accès illimité à 10,000+ cours de niveau international, projets pratiques et programmes de certification prêts à l'emploi - tous inclus dans votre abonnement.
Faites progresser votre carrière avec un diplôme en ligne
Obtenez un diplôme auprès d’universités de renommée mondiale - 100 % en ligne
Rejoignez plus de 3 400 entreprises mondiales qui ont choisi Coursera pour les affaires
Améliorez les compétences de vos employés pour exceller dans l’économie numérique
Foire Aux Questions
Pour accéder aux supports de cours, aux devoirs et pour obtenir un certificat, vous devez acheter l'expérience de certificat lorsque vous vous inscrivez à un cours. Vous pouvez essayer un essai gratuit ou demander une aide financière. Le cours peut proposer l'option "Cours complet, pas de certificat". Cette option vous permet de consulter tous les supports de cours, de soumettre les évaluations requises et d'obtenir une note finale. Cela signifie également que vous ne pourrez pas acheter un certificat d'expérience.
Lorsque vous achetez un certificat, vous avez accès à tous les supports de cours, y compris les devoirs notés. Une fois le cours terminé, votre certificat électronique sera ajouté à votre page de réalisations - à partir de là, vous pouvez imprimer votre certificat ou l'ajouter à votre profil LinkedIn.
Oui, pour certains programmes de formation, vous pouvez demander une aide financière ou une bourse si vous n'avez pas les moyens de payer les frais d'inscription. Si une aide financière ou une bourse est disponible pour votre programme de formation, vous trouverez un lien de demande sur la page de description.
Plus de questions
Aide financière disponible,
¹ Certains travaux de ce cours sont notés par l'IA. Pour ces travaux, vos Données internes seront utilisées conformément à Notification de confidentialité de Coursera.

