Linear algebra and calculus are the two most important foundational pillars on which modern mathematics is built. They are studied by almost all mathematics students at university, though typically labelled as different subjects and taught in parallel. Over time, students discover that linear algebra and calculus are inseparable (but not identical) twins that interlock to form the backbone of almost all applications of mathematics to physical and biological sciences, engineering and computer science. It is recommended that participants in the MOOC Introduction to Linear Algebra have already taken, or take in parallel, the MOOC Introduction to Calculus.



Introduction to Linear Algebra

Instructeur : David Easdown
Enseignant de premier plan
6 380 déjà inscrits
Inclus avec 
(26 avis)
Détails à connaître

Ajouter à votre profil LinkedIn
28 devoirs
Découvrez comment les employés des entreprises prestigieuses maîtrisent des compétences recherchées


Obtenez un certificat professionnel
Ajoutez cette qualification à votre profil LinkedIn ou à votre CV
Partagez-le sur les réseaux sociaux et dans votre évaluation de performance

Il y a 4 modules dans ce cours
This module introduces and explores the useful and elegant arithmetic of geometric vectors, regarded as directed line segments, which move about freely in the plane and in space. Objects in this arithmetic are ubiquitous throughout the physical world, modelling vector quantities. Students acquire tools that enable them to explore precise geometrical relationships between objects, prove difficult theorems and solve optimisation problems. This arithmetic forms a prototype for the general and abstract theory of vector spaces, developing students’ intuition and preparing them for advanced courses on linear algebra.
Inclus
10 vidéos11 lectures10 devoirs
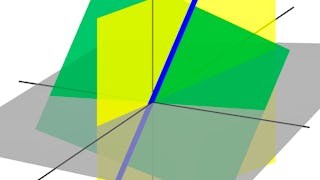
This module introduces and develops fluency with lines and planes in space, represented by vector and Cartesian equations. Students learn how to exploit the arithmetic of geometric vectors to solve difficult optimisation problems such as finding the closest point to a plane or finding the closest points on a pair of skew lines. The module introduces systems of linear equations and then develops the method of Gaussian elimination, using elementary row operations, followed by back substitution, to express solutions in terms of parameters. Systems of equations are also explored and solved using modular arithmetic with respect to a given prime number.
Inclus
8 vidéos6 lectures7 devoirs
This module introduces matrix arithmetic and the theory of determinants. Students first learn how to add matrices of the same size and how to multiply by a scalar. They then learn how to multiply matrices of compatible sizes, using cascades of dot products of rows with columns. This is described succinctly using Sigma notation, which is then used to prove associativity of matrix multiplication. Students learn about elementary matrices, which are basic building blocks in matrix arithmetic, closely related to elementary row operations used in Gaussian elimination. Students learn about matrix inverses and how to find them. Students learn about determinants and their properties, including the multiplicative property and a simple criterion for recognising invertibility of a matrix. Students see applications to cross products of vectors and for exploring spatial relationships between points and triangles.
Inclus
11 vidéos5 lectures5 devoirs
This module continues the development of matrix arithmetic by introducing eigenvalues and associated eigenvectors. Interpreted geometrically, these allow one to find directions in which a given linear operator associated with a matrix moves vectors in straight lines. This leads to the technique of diagonalisation, enabling one to solve difficult problems in matrix arithmetic, including finding formulae for powers of a given square matrix. This has many applications, including, for example, in exploring the behaviour of a Markov process described by a stochastic matrix, the mathematics of which underlies search engines on the internet. Eigenvalues can be found, in principle, by solving the characteristic equation of a matrix. Associated eigenvectors can then be found by solving an associated homogeneous system of equations. In practice, there are iterative numerical techniques for finding approximations of eigenvalues and eigenvectors, using a technique associated with Perron’s Theorem. Diagonalisation is a manifestation of the general Conjugation Principle, explored in different contexts. Linear transformations are introduced, focusing on transformation of the plane. Rotations and reflections of the plane combine to form the two-dimensional orthogonal group. Scalar dilations and rotations combine to form a copy of the field of complex numbers. A sketch of Smale’s proof of the Fundamental Theorem of Algebra is given, which says that any nonconstant polynomial with complex coefficients has a complex root, so that all square matrices have eigenvalues, when working over the field of complex numbers.
Inclus
13 vidéos6 lectures6 devoirs
Instructeur

Offert par
Recommandé si vous êtes intéressé(e) par Math and Logic


Johns Hopkins University

Johns Hopkins University


Howard University


Johns Hopkins University
Pour quelles raisons les étudiants sur Coursera nous choisissent-ils pour leur carrière ?




Avis des étudiants
26 avis
- 5 stars
84,61 %
- 4 stars
15,38 %
- 3 stars
0 %
- 2 stars
0 %
- 1 star
0 %
Affichage de 3 sur 26
Révisé le 1 nov. 2024
Excellent, challenging course. I had a lot of fun, thank you Prof. Easdown, and I am looking forward to taking your next courses!
Révisé le 6 juil. 2024
Thank you Professor Easdown. Look forward to more math courses from you
Révisé le 18 mai 2024
Grazie mille per questo corso bellissimo. Grazie al professore!
Thank you very much for this beautiful course!


Ouvrez de nouvelles portes avec Coursera Plus
Accès illimité à 10,000+ cours de niveau international, projets pratiques et programmes de certification prêts à l'emploi - tous inclus dans votre abonnement.

Faites progresser votre carrière avec un diplôme en ligne
Obtenez un diplôme auprès d’universités de renommée mondiale - 100 % en ligne

Rejoignez plus de 3 400 entreprises mondiales qui ont choisi Coursera pour les affaires
Améliorez les compétences de vos employés pour exceller dans l’économie numérique
Foire Aux Questions
Access to lectures and assignments depends on your type of enrollment. If you take a course in audit mode, you will be able to see most course materials for free. To access graded assignments and to earn a Certificate, you will need to purchase the Certificate experience, during or after your audit. If you don't see the audit option:
The course may not offer an audit option. You can try a Free Trial instead, or apply for Financial Aid.
The course may offer 'Full Course, No Certificate' instead. This option lets you see all course materials, submit required assessments, and get a final grade. This also means that you will not be able to purchase a Certificate experience.
When you enroll in the course, you get access to all of the courses in the Specialization, and you earn a certificate when you complete the work. Your electronic Certificate will be added to your Accomplishments page - from there, you can print your Certificate or add it to your LinkedIn profile. If you only want to read and view the course content, you can audit the course for free.
If you subscribed, you get a 7-day free trial during which you can cancel at no penalty. After that, we don’t give refunds, but you can cancel your subscription at any time. See our full refund policy.

