Ce cours porte sur les matrices et couvre de manière concise l'algèbre linéaire qu'un ingénieur doit connaître. Les mathématiques dans ce cours sont présentées au niveau d'un étudiant avancé du secondaire, mais il est recommandé que les étudiants suivent ce cours après avoir terminé un cours de calcul à une variable de niveau universitaire, tel que l'offre Coursera Calculus for Engineers. Il n'y a pas de dérivées ou d'intégrales impliquées, mais les étudiants sont censés avoir un niveau de maturité mathématique de base. Malgré cela, toute personne intéressée par l'apprentissage des bases de l'algèbre matricielle est la bienvenue. Le cours se compose de 38 vidéos de conférence concises, chacune suivie de quelques problèmes à résoudre. Chaque sujet principal est suivi d'un court quiz d'entraînement. Les solutions aux problèmes et aux quiz d'entraînement se trouvent dans les notes de cours fournies par l'enseignant. Le cours s'étend sur quatre semaines, et à la fin de chaque semaine, il y a un quiz évalué. Téléchargez les notes de cours à partir du lien https://www.math.hkust.edu.hk/~machas/matrix-algebra-for-engineers.pdf et regardez la vidéo promotionnelle à partir du lien https://youtu.be/IZcyZHomFQc

Algèbre matricielle pour les ingénieurs

Algèbre matricielle pour les ingénieurs
Ce cours fait partie de Spécialisation "Mathématiques pour ingénieurs"
Enseigné en Français (doublage IA)

Instructeur : Jeffrey R. Chasnov
Enseignant de premier plan
121 641 déjà inscrits
Inclus avec
4,643 avis
Expérience recommandée
Ce que vous apprendrez
Multiplication de matrices, transposition, inverse, matrices orthogonales
Élimination gaussienne, forme d'échelon à rangs réduits, décomposition LU
Espaces vectoriels, indépendance linéaire, processus de Gram-Schmidt, espace nul, espace des colonnes, problème des moindres carrés
Déterminants, expansion de Laplace, formule de Leibniz, problème des valeurs propres, diagonalisation des matrices, puissances d'une matrice
Compétences que vous acquerrez
- Catégorie : Mathématiques générales
- Catégorie : Mathématiques avancées
- Catégorie : Analyse technique
- Catégorie : Logique computationnelle
- Catégorie : Algèbre
- Catégorie : Mathématiques appliquées
- Catégorie : Calculs d'ingénierie
- Catégorie : Algèbre linéaire
- Catégorie : Arithmétique
Détails à connaître

Ajouter à votre profil LinkedIn
17 devoirs
Découvrez comment les employés des entreprises prestigieuses maîtrisent des compétences recherchées

Élaborez votre expertise du sujet
- Apprenez de nouveaux concepts auprès d'experts du secteur
- Acquérez une compréhension de base d'un sujet ou d'un outil
- Développez des compétences professionnelles avec des projets pratiques
- Obtenez un certificat professionnel partageable

Il y a 4 modules dans ce cours
Les matrices sont des tableaux rectangulaires de nombres, de symboles ou d'expressions, disposés en lignes et en colonnes. Nous définissons les matrices et montrons comment les additionner et les multiplier, nous définissons certaines matrices spéciales telles que la matrice identité et la matrice zéro, nous apprenons à connaître la transposition et l'inverse d'une matrice et nous discutons des matrices orthogonales et des matrices de permutation.
Inclus
10 vidéos26 lectures5 devoirs
Un système d'équations linéaires peut être écrit sous forme de matrice et peut être résolu à l'aide de l'élimination gaussienne. Nous apprenons à mettre une matrice sous forme d'échelon de rangée réduit, ce qui peut être utilisé pour calculer l'inverse de la matrice. Nous apprenons également à trouver la décomposition LU d'une matrice, et comment cette décomposition peut être utilisée pour résoudre efficacement un système d'équations linéaires dont les côtés droits changent.
Inclus
7 vidéos6 lectures3 devoirs
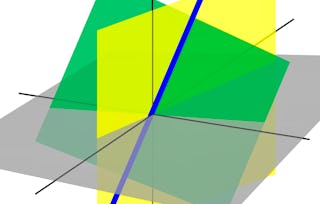
Un espace vectoriel est constitué d'un ensemble de vecteurs et d'un ensemble de scalaires, fermé par l'addition de vecteurs et la multiplication de scalaires et satisfaisant aux règles arithmétiques habituelles. Nous apprenons certains termes et expressions de l'algèbre linéaire, tels que l'indépendance linéaire, l'étendue, la base et la dimension. Nous apprenons à connaître les quatre sous-espaces fondamentaux d'une matrice, le processus de Gram-Schmidt, la projection orthogonale et la formulation matricielle du problème des moindres carrés consistant à tracer une ligne droite pour ajuster des données bruyantes.
Inclus
13 vidéos14 lectures5 devoirs
Un vecteur propre d'une matrice est un vecteur colonne non nul qui, lorsqu'il est multiplié par la matrice, n'est multiplié que par un scalaire (appelé valeur propre). Nous apprenons à connaître le problème des valeurs propres et à utiliser les déterminants pour trouver les valeurs propres d'une matrice. Nous apprenons à calculer les déterminants en utilisant l'expansion de Laplace, la formule de Leibniz et par élimination des lignes ou des colonnes. Nous apprenons également à diagonaliser une matrice en utilisant ses valeurs propres et ses vecteurs propres, et comment cela peut être utilisé pour calculer facilement une matrice élevée à une puissance.
Inclus
13 vidéos20 lectures4 devoirs1 plugin
Obtenez un certificat professionnel
Ajoutez ce titre à votre profil LinkedIn, à votre curriculum vitae ou à votre CV. Partagez-le sur les médias sociaux et dans votre évaluation des performances.
Instructeur

Enseignant de premier plan
En savoir plus sur Mathématiques et logique
 Statut : Essai gratuit
Statut : Essai gratuitJohns Hopkins University
 Statut : Essai gratuit
Statut : Essai gratuitThe Hong Kong University of Science and Technology
 Statut : Essai gratuit
Statut : Essai gratuitBirla Institute of Technology & Science, Pilani
 Statut : Essai gratuit
Statut : Essai gratuitJohns Hopkins University
Pour quelles raisons les étudiants sur Coursera nous choisissent-ils pour leur carrière ?

Felipe M.

Jennifer J.

Larry W.

Chaitanya A.
Avis des étudiants
- 5 stars
87,86 %
- 4 stars
10,50 %
- 3 stars
1,14 %
- 2 stars
0,19 %
- 1 star
0,30 %
Affichage de 3 sur 4643
Révisé le 7 juin 2020
Very good course its really useful and I learn so much through this course , thanks for all who is help us to learn more and more . The videos made me understand all the concepts.
Révisé le 16 avr. 2022
I found the explanations of prof Chesnoff very simple and informative. I understood much better the concepts of eigenvalues and vector spaces after chesnoffs' explanations!!!Thanks
Révisé le 17 oct. 2025
Great course overall, really helped to review many topics. I wish they talked more about the physical representation of matrices and vectors, but besides that, this course was great!

Ouvrez de nouvelles portes avec Coursera Plus
Accès illimité à 10,000+ cours de niveau international, projets pratiques et programmes de certification prêts à l'emploi - tous inclus dans votre abonnement.
Faites progresser votre carrière avec un diplôme en ligne
Obtenez un diplôme auprès d’universités de renommée mondiale - 100 % en ligne
Rejoignez plus de 3 400 entreprises mondiales qui ont choisi Coursera pour les affaires
Améliorez les compétences de vos employés pour exceller dans l’économie numérique
Foire Aux Questions
Pour accéder aux supports de cours, aux devoirs et pour obtenir un certificat, vous devez acheter l'expérience de certificat lorsque vous vous inscrivez à un cours. Vous pouvez essayer un essai gratuit ou demander une aide financière. Le cours peut proposer l'option "Cours complet, pas de certificat". Cette option vous permet de consulter tous les supports de cours, de soumettre les évaluations requises et d'obtenir une note finale. Cela signifie également que vous ne pourrez pas acheter un certificat d'expérience.
Lorsque vous vous inscrivez au cours, vous avez accès à tous les cours de la spécialisation et vous obtenez un certificat lorsque vous terminez le travail. Votre certificat électronique sera ajouté à votre page Réalisations - de là, vous pouvez imprimer votre certificat ou l'ajouter à votre profil LinkedIn.
Oui, pour certains programmes de formation, vous pouvez demander une aide financière ou une bourse si vous n'avez pas les moyens de payer les frais d'inscription. Si une aide financière ou une bourse est disponible pour votre programme de formation, vous trouverez un lien de demande sur la page de description.
Plus de questions
Aide financière disponible,

