Ce cours couvre à la fois les fondements théoriques et les applications pratiques du calcul vectoriel. Au cours de la première semaine, les étudiants apprendront à connaître les champs scalaires et vectoriels. Au cours de la deuxième semaine, ils différencieront les champs. La troisième semaine est consacrée à l'intégration multidimensionnelle et aux systèmes de coordonnées curvilignes. Les intégrales de lignes et de surfaces sont abordées au cours de la quatrième semaine, tandis que la cinquième semaine explore les théorèmes fondamentaux du calcul vectoriel, notamment le théorème du gradient, le théorème de la divergence et le théorème de Stokes. Ces théorèmes sont essentiels pour des sujets d'ingénierie tels que l'électromagnétisme et la mécanique des fluides. Notez que ce cours peut également être appelé Calcul multivariable ou Multivariate Calculus ou Calculus 3 dans certaines universités. La condition préalable à ce cours est d'avoir suivi deux semestres de calcul à une variable (différenciation et intégration). Le cours comprend 53 vidéos de cours concises, chacune suivie de quelques problèmes à résoudre. Après chaque grand sujet, il y a un petit quiz d'entraînement. A la fin de chaque semaine, il y a un quiz évalué. Les solutions aux problèmes et aux quiz d'entraînement se trouvent dans les notes de cours fournies par l'enseignant.

Calcul vectoriel pour les ingénieurs

Calcul vectoriel pour les ingénieurs
Ce cours fait partie de Spécialisation "Mathématiques pour ingénieurs"
Enseigné en Français (doublage IA)

Instructeur : Jeffrey R. Chasnov
Enseignant de premier plan
47 087 déjà inscrits
Inclus avec
1,405 avis
Expérience recommandée
Ce que vous apprendrez
Vecteurs, produit en points et produit en croix
Le gradient, la divergence, la courbure et le laplacien
Intégration multivariable, coordonnées polaires, cylindriques et sphériques
Intégrales de ligne, intégrales de surface, théorème du gradient, théorème de la divergence et théorème de Stokes
Compétences que vous acquerrez
- Catégorie : Produits dérivés
- Catégorie : Calculs
- Catégorie : Ingénierie mécanique
- Catégorie : Mathématiques appliquées
- Catégorie : Mécanique
- Catégorie : Analyse technique
- Catégorie : Génie électrique
- Catégorie : Calculs d'ingénierie
- Catégorie : Physique
- Catégorie : Calcul intégral
- Catégorie : électromagnétisme
- Catégorie : Mathématiques avancées
- Catégorie : Géométrie
- Catégorie : Ingénierie
- Section Compétences masquée. Affichage de 11 compétence(s) sur 14.
Détails à connaître

Ajouter à votre profil LinkedIn
20 devoirs
Découvrez comment les employés des entreprises prestigieuses maîtrisent des compétences recherchées

Élaborez votre expertise du sujet
- Apprenez de nouveaux concepts auprès d'experts du secteur
- Acquérez une compréhension de base d'un sujet ou d'un outil
- Développez des compétences professionnelles avec des projets pratiques
- Obtenez un certificat professionnel partageable

Il y a 5 modules dans ce cours
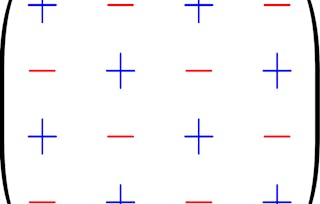
Les vecteurs sont des constructions mathématiques qui ont à la fois une longueur et une direction. Nous définissons les vecteurs et montrons comment les additionner et les soustraire, et comment les multiplier à l'aide des produits point et croix. Nous appliquons les vecteurs à l'étude de la géométrie analytique des lignes et des plans, et nous définissons le delta de Kronecker et le symbole de Levi-Civita pour prouver les identités vectorielles. Enfin, nous définissons les concepts importants de champs scalaires et vectoriels.
Inclus
15 vidéos27 lectures5 devoirs2 plugins
Les champs scalaires et vectoriels peuvent être différenciés. Nous définissons la dérivée partielle et dérivons la méthode des moindres carrés comme un problème de minimisation. Nous apprenons à utiliser la règle de la chaîne pour une fonction de plusieurs variables et dérivons la règle du triple produit utilisée en génie chimique. Nous définissons le gradient, la divergence, le curl et le laplacien. Nous apprenons quelques identités utiles du calcul vectoriel et les dérivons en utilisant le delta de Kronecker et le symbole de Levi-Civita. Nous utilisons les identités vectorielles pour dériver l'équation des ondes électromagnétiques de l'équation de Maxwell en espace libre. Les ondes électromagnétiques sont à la base de toutes les technologies de communication modernes.
Inclus
13 vidéos15 lectures4 devoirs
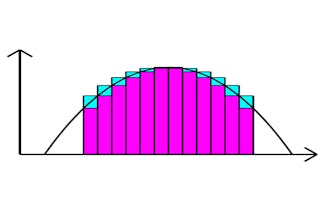
L'intégration peut être étendue aux fonctions de plusieurs variables. Nous apprenons à effectuer des intégrales doubles et triples. Nous définissons les coordonnées curvilignes, à savoir les coordonnées polaires en deux dimensions et les coordonnées cylindriques et sphériques en trois dimensions, et nous les utilisons pour simplifier les problèmes présentant une symétrie circulaire, cylindrique ou sphérique. Nous apprenons à écrire des opérateurs différentiels en coordonnées curvilignes et à changer de variables dans des intégrales multidimensionnelles en utilisant le jacobien de la transformation.
Inclus
12 vidéos24 lectures4 devoirs
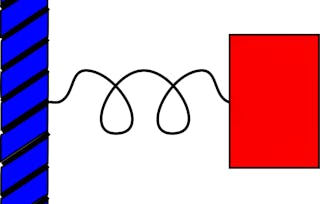
Les champs scalaires ou vectoriels peuvent être intégrés sur des courbes ou des surfaces. Nous apprenons à prendre l'intégrale de ligne d'un champ scalaire et à l'utiliser pour calculer les longueurs d'arc. Nous apprenons ensuite à prendre l'intégrale de ligne d'un champ vectoriel en prenant le produit point du champ vectoriel avec les vecteurs unitaires tangents à la courbe. L'examen de l'intégrale de ligne d'un champ de force aboutit au théorème travail-énergie. Ensuite, nous apprenons à prendre l'intégrale de surface d'un champ scalaire et à utiliser l'intégrale de surface pour calculer les surfaces. Nous apprenons ensuite à calculer l'intégrale de surface d'un champ de vecteurs en effectuant le produit de points du champ de vecteurs avec le vecteur normal unitaire à la surface. L'intégrale de surface d'un champ de vitesse est utilisée pour définir le flux de masse d'un fluide à travers une surface.
Inclus
9 vidéos11 lectures3 devoirs
Le théorème fondamental du calcul relie l'intégration à la différenciation. Nous apprenons ici les théorèmes fondamentaux du calcul vectoriel qui y sont liés. Il s'agit notamment du théorème du gradient, du théorème de la divergence et du théorème de Stokes. Nous montrons comment ces théorèmes sont utilisés pour dériver les équations de continuité et la loi de conservation de l'énergie. Nous montrons comment définir la divergence et le curl sous forme libre de coordonnées, et comment convertir la version intégrale des équations de Maxwell sous forme différentielle.
Inclus
13 vidéos21 lectures4 devoirs
Obtenez un certificat professionnel
Ajoutez ce titre à votre profil LinkedIn, à votre curriculum vitae ou à votre CV. Partagez-le sur les médias sociaux et dans votre évaluation des performances.
Instructeur

Enseignant de premier plan
En savoir plus sur Mathématiques et logique
 Statut : Prévisualisation
Statut : PrévisualisationThe Hong Kong University of Science and Technology
 Statut : Essai gratuit
Statut : Essai gratuitThe Hong Kong University of Science and Technology
 Statut : Prévisualisation
Statut : PrévisualisationKorea Advanced Institute of Science and Technology(KAIST)
 Statut : Essai gratuit
Statut : Essai gratuitThe Hong Kong University of Science and Technology
Pour quelles raisons les étudiants sur Coursera nous choisissent-ils pour leur carrière ?

Felipe M.

Jennifer J.

Larry W.

Chaitanya A.
Avis des étudiants
- 5 stars
83,71 %
- 4 stars
14,08 %
- 3 stars
1,28 %
- 2 stars
0,56 %
- 1 star
0,35 %
Affichage de 3 sur 1405
Révisé le 24 juil. 2020
Very good course with difficult problems. Very good instructor. Needs to provide a bit more geometric intuition to the sections involving vector integral calculus.
Révisé le 14 mai 2021
Professor Chasnov is a great instructor. I strongly recommend this course (and others from his). Thank you so much for making such great quality content available for everyone no matter where.
Révisé le 8 janv. 2021
A superbly presented course with excellent notes and examples. I will be using a number of concepts to extend my Advanced Programme Math classes I teach. Thank you!

Ouvrez de nouvelles portes avec Coursera Plus
Accès illimité à 10,000+ cours de niveau international, projets pratiques et programmes de certification prêts à l'emploi - tous inclus dans votre abonnement.
Faites progresser votre carrière avec un diplôme en ligne
Obtenez un diplôme auprès d’universités de renommée mondiale - 100 % en ligne
Rejoignez plus de 3 400 entreprises mondiales qui ont choisi Coursera pour les affaires
Améliorez les compétences de vos employés pour exceller dans l’économie numérique
Foire Aux Questions
Pour accéder aux supports de cours, aux devoirs et pour obtenir un certificat, vous devez acheter l'expérience de certificat lorsque vous vous inscrivez à un cours. Vous pouvez essayer un essai gratuit ou demander une aide financière. Le cours peut proposer l'option "Cours complet, pas de certificat". Cette option vous permet de consulter tous les supports de cours, de soumettre les évaluations requises et d'obtenir une note finale. Cela signifie également que vous ne pourrez pas acheter un certificat d'expérience.
Lorsque vous vous inscrivez au cours, vous avez accès à tous les cours de la spécialisation et vous obtenez un certificat lorsque vous terminez le travail. Votre certificat électronique sera ajouté à votre page Réalisations - de là, vous pouvez imprimer votre certificat ou l'ajouter à votre profil LinkedIn.
Oui, pour certains programmes de formation, vous pouvez demander une aide financière ou une bourse si vous n'avez pas les moyens de payer les frais d'inscription. Si une aide financière ou une bourse est disponible pour votre programme de formation, vous trouverez un lien de demande sur la page de description.
Plus de questions
Aide financière disponible,

